Recent developments in the asymptotic theory of separated flows - Leverhulme Lectures

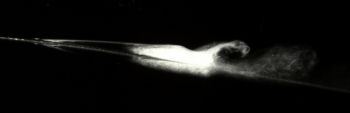
Transitional separation bubble.
Source: G. Cole, T.J. Mueller (Univ. Notre Dame, Indiana, USA)

Page contents

• Introduction
• Course contents
• Lecture Notes

Introduction

Although Prandtl's seminal contribution to the understanding of viscous flows at high Reynolds numbers dates back one century significant problems in the context of boundary layer separation and laminar-turbulent boundary layer transition remain still unsolved. The clarification of these open questions is desirable not only from a theoretical point of view but is also essential for practical purposes such as accurate numerical computations with a minimum amount of model assumptions.

A milestone in the development of boundary layer theory is, among others, the introduction of viscous-inviscid interaction by Neiland, Stewartson, Williams and Messiter 1969/70. This approach turned out to be very successful in the description of various fundamental flow problems but could not resolve Goldstein's singularity associated with (strong) boundary layer separation, Stewartson 1970. However, as demonstrated by Ruban 1981 and Stewartson, Smith and Kaups 1982 the strength of Goldstein's singularity can be reduced by varying a parameter controlling the pressure gradient acting on the boundary layer. The limiting case of so-called marginal separation can then be treated successfully with the interaction concept and enables the description of small reverse flow regions. While steady flow problems of this type seemed to be analyzed adequately, another breakdown in the form of finite time blow-up appeared in the investigations of the equation of marginal separation extended to include unsteady effects. This breakdown then was associated with a sudden change of the global flow structure.

However, more recent investigations with special emphasis on the well-known non-uniqueness and branching behavior of steady solutions showed that in the vicinity of the bifurcation point unsteady three-dimensional perturbations of the flow field are governed by an evolution equation of Fisher's type known from mathematical biology. The existence of singular travelling waves interpreted as vortex sheets suggest that solutions of the Fisher equation leading to the formation of finite time singularities may be extended beyond the blow-up time, thereby generating vortical structures qualitatively similar to those emerging in direct numerical simulations and experimental investigations of transitional separation bubbles.

The course is supported by The Leverhulme Trust and The Manchester Institute of Mathematical Sciences

Lecture contents

1. Classical boundary layer theory and its breakdown:

motivation, second order theory, displacement effect, example: flow past airfoil, behavior near a point of vanishing skin friction

2. The concept of viscous/inviscid interaction (triple deck) - flat plate trailing edge flow:

local analysis, interaction

3. Marginal separation:

experimental observations, DNS results, benchmark problem: channel flow, theory of marginal separation (classical boundary layer at the verge of separation, interaction), extension to unsteady, three-dimensional interacting flow including control devices, bifurcation analysis, flow control

4. Fisher's equation:

sub/supercritical flow conditions, singular travelling waves, numerics, blow-up asymptotics

5. Bifurcations in triple deck flows:

subsonic ramp and trailing edge flows, adjoint approach, flow symmetry considerations

Lecture Notes

• Final Version (3rd August 2006): MIMS EPrint 2006.226, Manchester Institute for Mathematical Sciences, The University of Manchester, UK, August 2006.